
Hello again! Welcome to the follow-up blog from the previous one where we discussed How Solar Radiation Pressure Affects Satellites: Calculating Instantaneous Force and Acceleration. As the title suggests, this time we’ll dive deeper into understanding how to calculate long-term orbital perturbations due to solar radiation pressure.
This is a vast topic, but my goal is to simplify it as much as possible for everyone. These blogs are aimed at providing a foundational introduction to the fascinating realm of orbital mechanics.
Now, I have a confession—if you’re a mathematician or physicist, can we have a video call? Sometimes I wonder if I should have pursued Astrophysics instead of diving into AI and Robotics. ? Just kidding! I’m much better in this field, and I can’t imagine myself knee-deep in equations with Einstein-style hair. At least, I like to think I’m cool… Please don’t get offended by my nerdy jokes!
Alright, enough yapping—let’s get back to the topic. To quickly recap what we discussed in the last blog:
Solar radiation pressure is the force exerted by photons emitted by the Sun when they strike a satellite’s surface. The magnitude of this pressure depends on:
- The satellite’s cross-sectional area exposed to sunlight,
- The reflectivity of its surfaces,
- Its orientation relative to the Sun,
- And its distance from the Sun (though for low Earth orbit, this is usually assumed constant).
While the force from solar radiation pressure is small, over time it can cause significant changes in a satellite’s orbital elements. In the last blog, we focused on calculating the immediate effect of this pressure, but not how it accumulates and affects the spacecraft over time.
This blog will cover exactly that.
To make it more realistic and understandable, we’ll use EIRSAT-1 as a case study—one of the most well-known student-led CubeSat missions, launched by the students of University College Dublin as part of the European Space Agency’s Fly Your Satellite! programme.
I didn’t find extensive details about the mission (Wikipedia had some info, but we all know how trustworthy that is), so I gathered what I could from official publications and real-time data from the n2yo website. As always, I’ll provide links below for anyone who wants to fact-check.
Now, let’s get all the information down properly and begin!
| EIRSAT-1 Satellite Data | |
|---|---|
| Latitude | -41.18° |
| Longitude | 74.18° |
| Altitude | 481.19 km (299 mi) |
| Speed | 7.62 km/s (4.73 mi/s) |
| Azimuth | 232.0° SW |
| Elevation | -55° |
| Right Ascension | 07h 51m 50s |
| Declination | -60° 20′ 10” |
| Launch Mass | 2.305 kg |
| Dimensions | 10.67 cm × 10.67 cm × 22.7 cm (4.20 in × 4.20 in × 8.94 in) |
| Satellite Period | 94 minutes |
Now we have the data let’s try to understand how and what steps are we going to take also before that let’s list down the factors to consider when calculating the effect of solar radiation pressure on an object:
Factors to Consider for Solar Radiation Pressure Calculations:
Orbital Elements:
- Semi-major axis
- Eccentricity
- Inclination
- Right Ascension of Ascending Node (RAAN)
- Argument of Perigee
- True Anomaly
- Mean Anomaly
- Eccentric Anomaly
Satellite Geometry:
- Cross-sectional area
- Reflectivity data
Material Properties:
- Absorptivity and emissivity
- Degradation rates over time
Orientation Data:
- The satellite’s attitude and orientation over time
Distance to the Sun:
- Updated regularly throughout the year to account for orbital variations
Step-by-Step Calculation
Solar Radiation Pressure Calculation
We already know the formula for calculating solar radiation pressure:

Determine the Cross-Sectional Area: Using the dimensions of
EIRSAT-1 (10.67 cm × 10.67 cm × 22.7 cm), the cross-sectional area facing the Sun (depending on its orientation) could be approximated. For the largest face:
![]()
Force on the Satellite Due to Solar Radiation Pressure
We’ll calculate the force exerted by solar radiation pressure using the following formula:
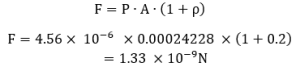
Instantaneous Acceleration on the Satellite Due to Solar Radiation Pressure
We can calculate the acceleration using Newton’s second law:
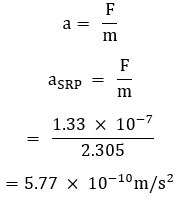
Atmospheric Drag Force Formula
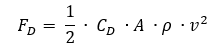
FD is the drag force in Newtons,
CD is the drag coefficient (typically between 2.0 and 2.5 for satellites),
A is the cross-sectional area of the satellite (0.00024228 m2),
ρ is the atmospheric density at the satellite’s altitude,
v2 is the satellite’s velocity relative to the atmosphere (7.69 km/s).
Now we don’t know what is Atmospheric Density for that point of time so I used
NRLMSISE 2.0 is an empirical, global reference atmospheric model of the Earth from ground to space. It models the temperatures and densities of the atmosphere’s components.
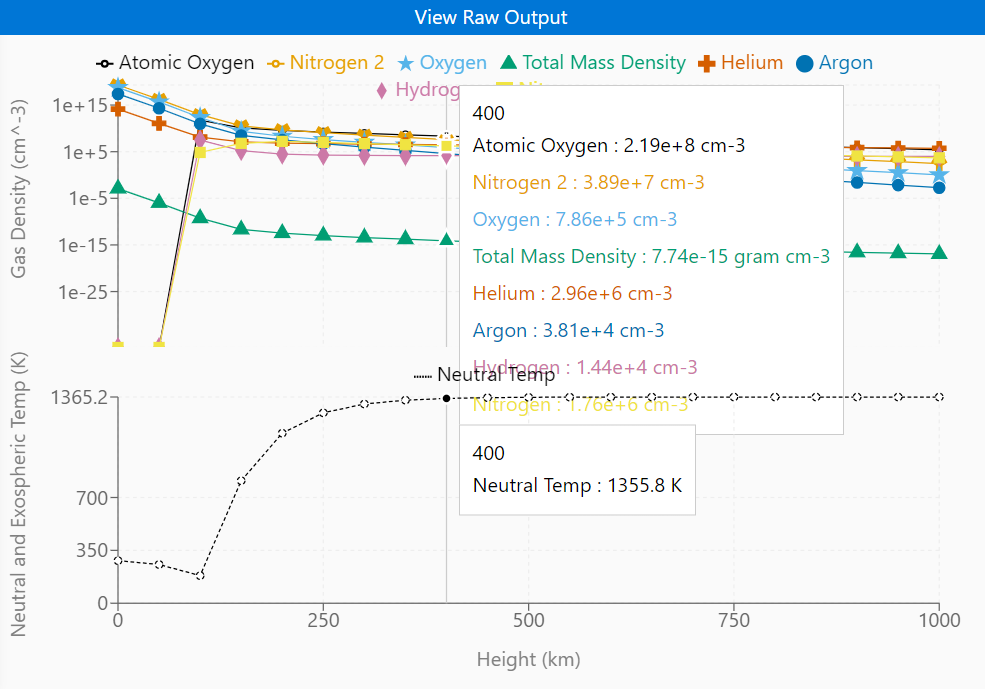
Now we get,
![]()
let’s substitute it in the formula
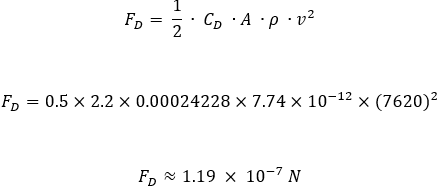
Acceleration due to Drag
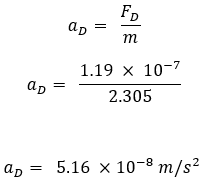
Now Finally,
Lagrange’s Planetary Equations:
You might wonder why we still need to use Lagrange’s planetary equations when we’ve already calculated the forces acting on the satellite. These equations allow us to determine how the orbital elements of a satellite (such as semi-major axis, eccentricity, inclination, and others) change over time due to external forces.
Since the focus of this blog is to calculate long-term orbital perturbations, Lagrange’s planetary equations provide a structured way to analyse the cumulative effects of small forces like solar radiation pressure (SRP) and atmospheric drag. They give us a clear picture of how a satellite’s orbit evolves over extended periods.
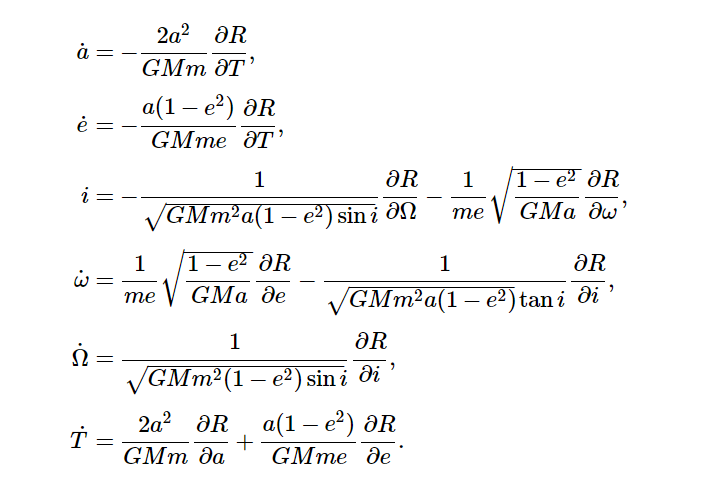
Above are the formulas for the Lagrange’s Planetary Equations where
ȧ is the Semi-major Axis
ė is the Eccentricity
i̇ is the Inclination
ω̇ is the Argument of Perigee
Ω̇ is the Right Ascension of the Ascending Node
Ṫ is the Time (Orbital Period)
I will be creating a separate blog dedicated to solving these equations in detail. If you have the necessary data for your own satellite, you’ll be able to input it into the equations and follow along to solve for long-term orbital changes.
Disclaimer: I am not a mathematician or physicist; the information presented here is sourced from various online references, which I have linked below. If you have any suggestions or feedback, feel free to reach out to me at ppadole@imperial.ac.uk ?
References
General Perturbation Theory – Lagrange’s Planetary Equations, LibreTexts
Lagrange’s Planetary Equations, ASU Control Systems
EIRSAT-1 Conferences, EIRSAT-1 Official Website