I came across a LinkedIn post by a postdoctoral researcher working on something interesting. The first thing that caught my eye was his list of research interests. I always thought someone should focus on one specific domain like biology or physics and explore subfields within that. But this researcher was working at the intersection of mathematics, physics, and computer science.
That one word “intersection” clicked something in me. I realized it was possible to combine different interests in a meaningful way. I messaged him on LinkedIn, not really expecting a reply. After all, I was an undergrad from a different background, and he must have gotten a lot of messages. But to my surprise, he responded within minutes.
We scheduled a Zoom call for March 27th, 2025, and though I was excited, I had no clue what “Lean” was, or what “theorem proving” meant. I asked a few friends studying physics at Imperial to explain, and after some Googling, it started to make sense.
So, What Is Lean and Theorem Proving?
Let me explain it the way it started to make sense to me.
Take something simple:
“Every time I flip this switch, the light turns on.”
In everyday life, we’d just accept that as true. We’ve seen it happen. But a theorem prover like Lean doesn’t take your word for it.
It’s like a robot that says:
“Prove it. Show me the wiring, the power source, the bulb, the laws of electricity. No skipping.”
If you can explain every single logical step, it’ll say:
“Yes, this is probably true.”
But if something’s missing:
“Nope. Try again.”
It feels like overkill at first. But it starts to make sense when you think about systems where guessing or assuming just isn’t good enough.
Where Is This Actually Used?
Imagine the light switch isn’t just in your bedroom, it’s a switch on a rocket.
- “If the engine overheats, it shuts down safely.”
- “If a pacemaker detects a problem, it responds in under a second.”
- “If someone tries to hack the system, no data is leaked.”
In cases like these, ‘it worked when we tested it’ isn’t always enough. You need guarantees. That’s where formal verification and tools like Lean 4 comes in.
Meeting Dr. Joseph and Learning About PhysLean
That first Zoom call with Dr. Joseph really stayed with me. He turned out to be kind, welcoming, and genuinely interested in helping someone new understand the field. I thought the call might last 15 minutes. We ended up talking for over an hour. He even shared stories about his work at Reykjavik University in Iceland.
That conversation is what led me to PhysLean.
What Is PhysLean?
If you’ve heard of mathlib, the formal math library built using Lean PhysLean is like its physics counterpart.
It’s an open-source library being developed in Lean 4, aiming to formalize major areas of physics in a way that computers can read, check, and reason through. It already includes areas like electromagnetism, condensed matter physics, classical mechanics, and quantum field theory and continues to grow.
The goal is to create a structured, formal foundation for physics where:
- Every law is written in a language a computer can understand
- Every equation is logically derived from first principles
- Every assumption is made explicit

Physics, as practiced, often hides small errors, forgotten approximations, missing units, implicit assumptions. Famously, NASA lost a $125 million Mars orbiter due to a simple unit conversion error.
Why It Matters
PhysLean is still in development, its potential spans research, engineering, and education:
- In self-driving cars, control systems could be proven safe, not just empirically tested.
- In quantum research, highly complex models could be logically verified.
- In education, students wouldn’t just use formulas, they’d see the logic behind them, step by step.
It’s not about replacing physics research, it’s about strengthening it.
What’s Next?
Since that first call, I’ve had more conversations with Dr. Joseph. We finally met in person at Imperial College London on June 13th. He shared that from September 2025, he’ll be joining the University of Bath as an Assistant Professor, where he plans to continue developing PhysLean and growing a lab around it.
It’s still early days for me, but that one LinkedIn post really did shift how I think about physics, programming, and what research can look like at the intersection of different fields.

Learn More
There’s much more to come with PhysLean. You can find more information below:
PhysLean Website: https://physlean.com/
GitHub: https://github.com/HEPLean/PhysLean
Dr. Joseph Tooby – Smith’s website: https://josephtoobysmith.com/


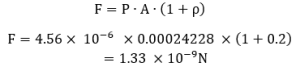
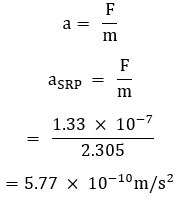
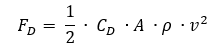
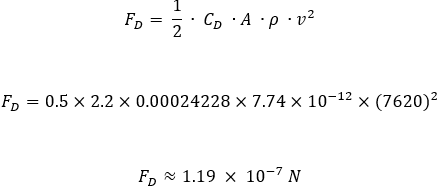
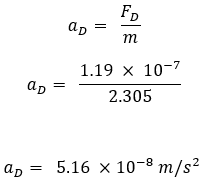
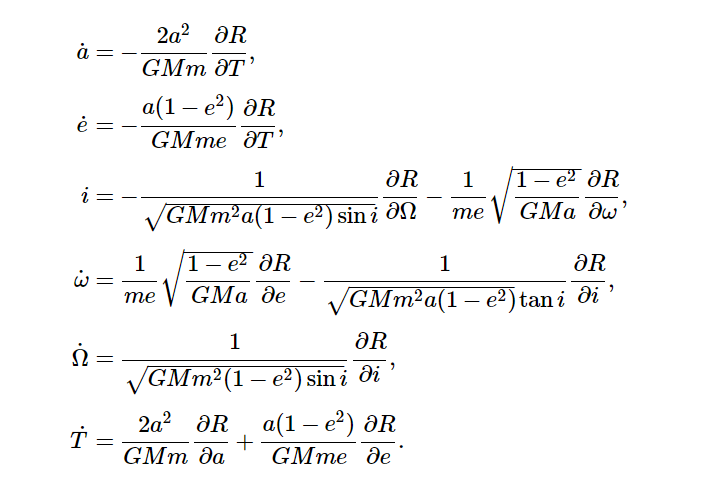
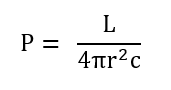 Where
Where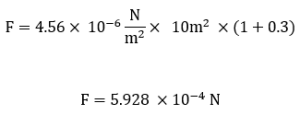 So, the instantaneous force acting on the satellite due to solar radiation pressure is F=5.928 ×10^(-4) N
So, the instantaneous force acting on the satellite due to solar radiation pressure is F=5.928 ×10^(-4) N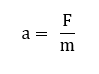 Where:
Where: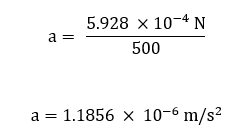 Although the force and acceleration caused by solar radiation pressure are small, they are persistent. Over time, they can lead to measurable changes in the satellite’s trajectory, especially for satellites with large area-to-mass ratios. For lightweight satellites, like CubeSats, solar radiation pressure can become a dominant factor affecting their orbits.
Although the force and acceleration caused by solar radiation pressure are small, they are persistent. Over time, they can lead to measurable changes in the satellite’s trajectory, especially for satellites with large area-to-mass ratios. For lightweight satellites, like CubeSats, solar radiation pressure can become a dominant factor affecting their orbits.