
Is it possible to control a robot without a model that describes its kinematics?
Author: Ahmad AlAttar
[1] Ahmad AlAttar and Petar Kormushev, “Kinematic-Model-Free Orientation Control for Robot Manipulation Using Locally Weighted Dual Quaternions”, In Robotics, vol. 9, no. 3, pp. 1-16, 2020. | Read the full paper | Download the PDF
Introduction
From the very first industrial robots to the more recent cobots, model-based approaches have remained the prevalent control method for over half a century. Conventional control of robotic systems, such as manipulators, is based on the kinematics and dynamics of rigid bodies that use joint-space to task-space transformations to calculate their poses. Once set, any change in the robot’s structure or environment is unwelcome!
What if the robot was slightly damaged? What if the robot’s structure changed or evolved? What if it was new robot that has not been modelled yet? What if a load was suddenly attached to the robot making it heavier? Simply put, what if something changes? Using conventional model-based approaches will not work. That is where our kinematic-model-free (KMF) controller shines!
Kinematic-Model-Free Position Control
The controller begins by collecting minimal information by applying pseudorandom torques to the joints and recording the displacements caused to the end effector. This memory is then used to build a local linear model which represents the locally combined kinematics and dynamics of the robot. Finally, this model is used to calculate the toques required to actuate the end-effector towards a desired target. All future movements are also recorded. A subset of the memory closest to the end-effector’s current position is then used for succeeding actuations. After each step, the desired and actual end-effector displacements are compared. Should there be a high discrepancy due to model inaccuracies, another exploratory phase is triggered. It’s as simple as that! The whole process can be summarised in the following flowchart:
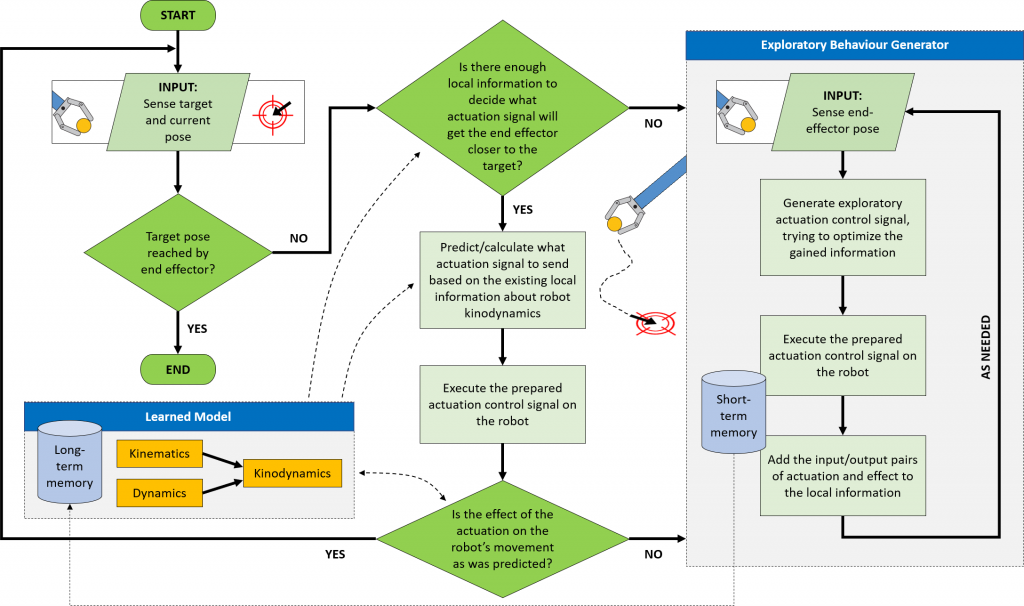
A flowchart describing Kinematic-Model-Free Control [1].
KMF position control can be applied to any robot, without knowing anything about the robot’s kinematics! Here are some examples in simulation:
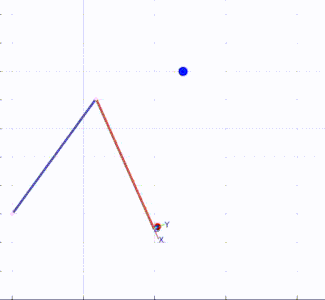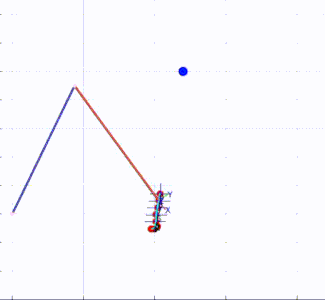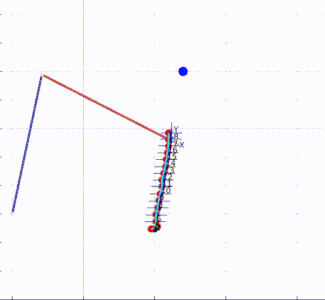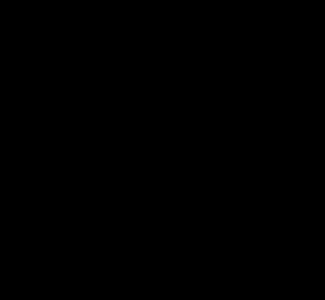
KMF position control applied to a 2 DOF robot.
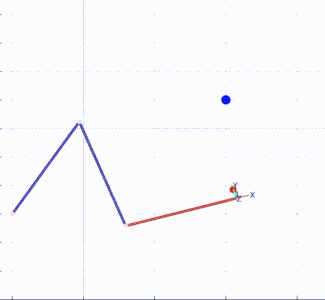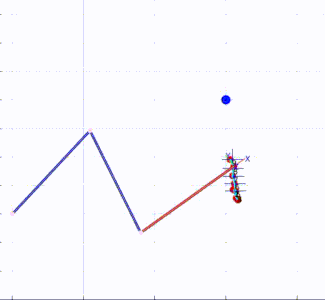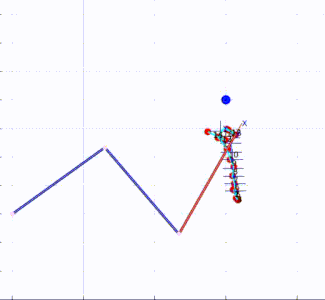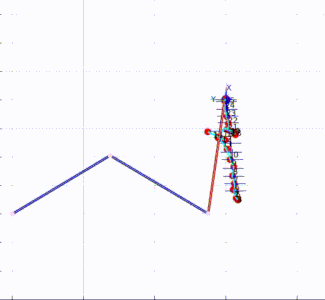
KMF position control applied to a 3 DOF planar robot.
KMF position control applied to a 3 DOF robot that moves in 3D space.
Here’s Kinematic-Model-Free position control working in the real world:
KMF position control applied to a 3 DOF planar robot in the real world.
Kinematic-Model-Free Orientation Control
The challenge with orientation control is how to represent orientation without discontinuities. For example, let’s say a planar robot’s end effector has to go to 190 degrees. The robot starts from 0 degrees. The controller starts exploring and eventually moves towards 180 degrees. Once the robot attempts to cross the 180 degrees mark, due to the [-180,+180] orientation range, the controller will read a sudden -180; this will trigger exploration. We could have commanded -170 instead of 190 degrees. However, what if the robot starts at 145 degrees? It will take the longer way around to reach to -170.
These problems can be overcome if we use quaternions to represent orientation. Quaternions are an extension to the complex number system used to represent rotations, first described by Hamilton around 1844. A quaternion consists of a scalar term, and a vector:

Since orientation control on its own is of little interest to roboticists, dual-quaternions, which are an extension to the dual number system used to represent rigid transformations by unifying rotational and translational information into a single mathematical object, are used. The dual quaternion representing position and orientation is comprised of two quaternions; r, the orientation quaternion, and t, the translation quaternion:

Now, all joint torques are mapped to relative dual-quaternions (combined translational and rotational displacements). These tuples are used to build a local linear model using Dual-Quaternion Linear Combinations. The controller (KMF-DQ) then calculates the required joint torques for a desired translation and rotational displacement using Dual-Quaternion Regression.
Results
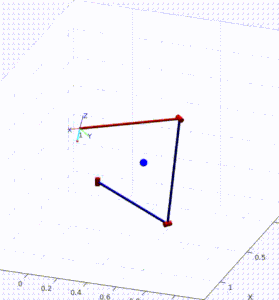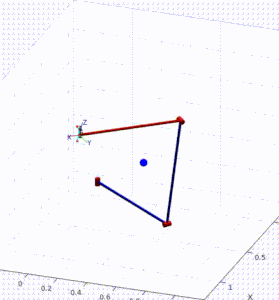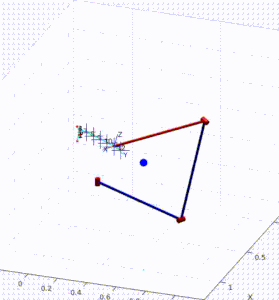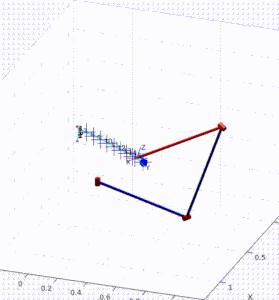
A dynamic simulation of a 3-DoF robot was performed in MATLAB. The KMF-DQ controller performed a set reaching tasks. The controller had to move the robot’s end effector to four target poses, drawing a polygon in 3D space.
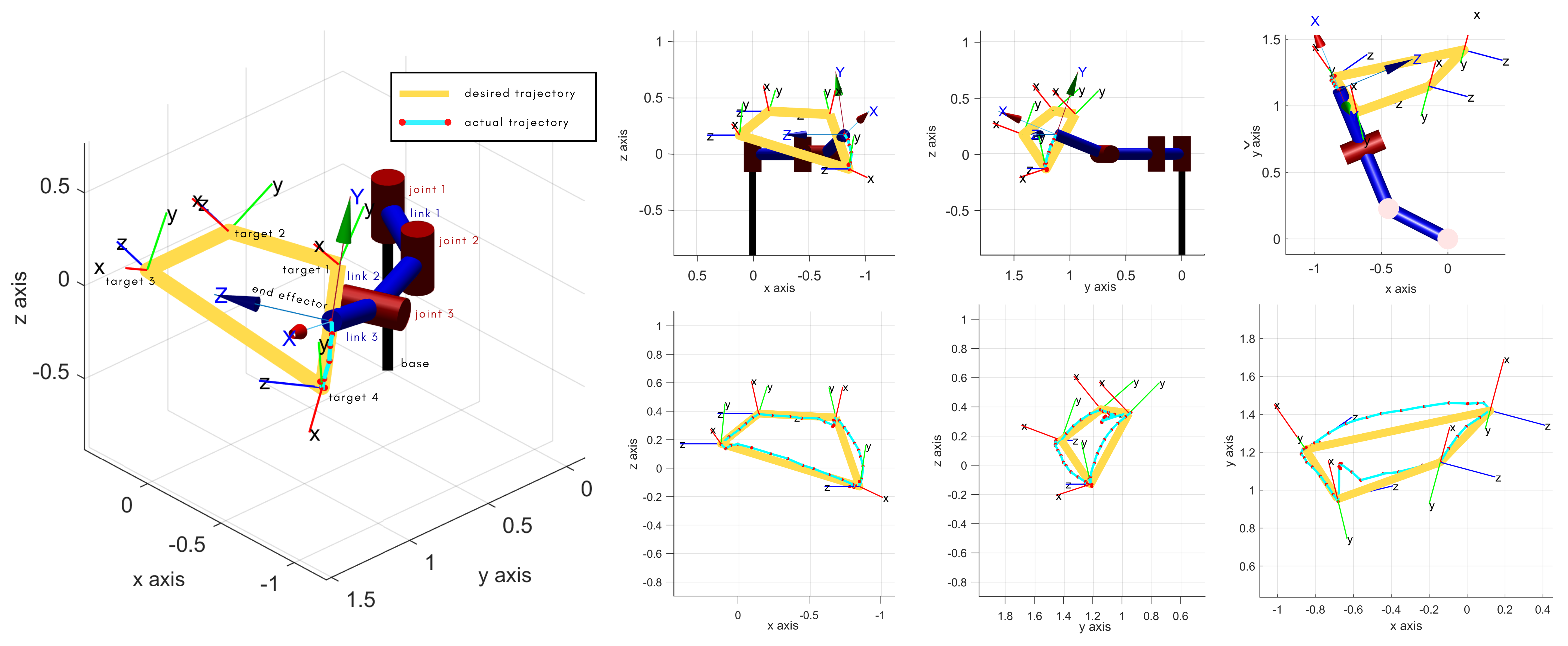
Results of KMF-DQ control in simulation.
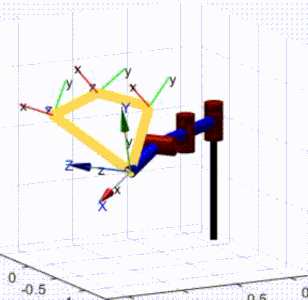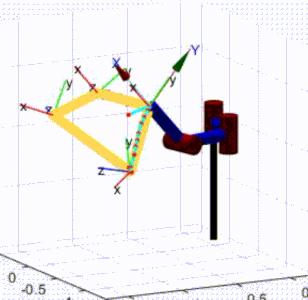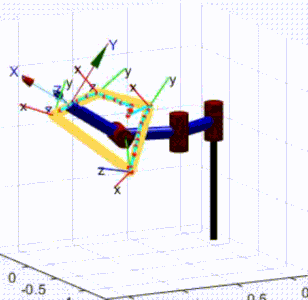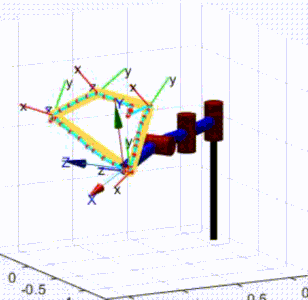
KMF-DQ controller in action.
The KMF-DQ controller generates intermediate targets to follow the yellow trajectory. The robot successfully reaches all four target poses, drawing the polygon in 3D space. These results prove that the local information of the robot is sufficient to create a local model that can be used to actuate the end effector towards a given target.
Although not guaranteed, the simulation demonstrated convergence to the desired targets. The controller’s robustness was measured by running the simulation 100 times, each with a random starting robot configuration and a randomly placed target pose within the robot’s reachable workspace that is achievable within 100 steps. The target poses lie within the robot’s achievable configuration space. It was found that 87% of the time, the controller successfully performed the reaching task. In the remaining 13%, the controller did not converge to solutions that actuate the robot towards the targets.
The proposed approach looks promising and can be used in applications where simultaneous translational and rotational reaching is required. This approach can be used for new robot designs where a model is not present and where flexibility is favoured over precision and speed.