We will briefly discuss zeros and poles of meromorphic functions here. We assume the Laurent series exist in the vicinity of a point z0:

Clearly if we want f(z0) is zero we require ak is zero for k smaller and equals to zero. Consequently we define that z0 is a zero of order n if:
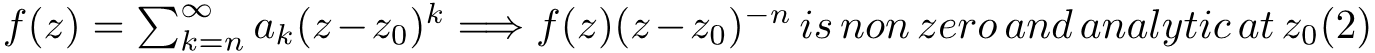
We can observe some useful properties from (2). Firstly, an n order zero implies that up to the (n-1)th derivative of f(z) are also zero at z0 and vice versa. We can use this property to determine the order of zeros of a function, in the case that they are not so obvious. Secondly, The zeros of f(z) are the poles of 1/f(z) for obvious reason, provided that f(z) is not identically zero. We would like to find the properties of the Laurent series of 1/f(z):
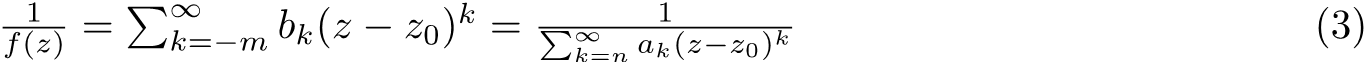
The value of m can be determined by multiply the denominator of right hand side : We obtain a series that constantly equals to one. This requires m=n, and we see the coefficients bk are fixed by the values of ak .
In summary we found that
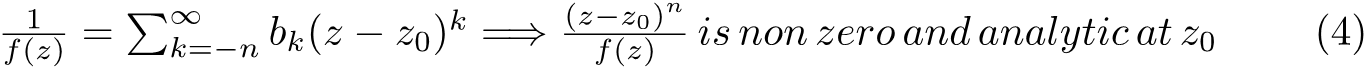
In particular, if f(z) is analytic and non-zero at z0 , we now from (2) know that n=0 and thus from (4) 1/f(z) is also analytic and non-zero at z0.