1. Weierstrass Approximation Theorem
We want to show that The set of polynomials is dense in the space of continuous functions. We shall firstly define the Bernstein Polynomials as
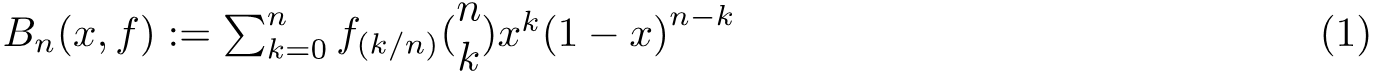
where f is a continuous function with domain [0,1] and we can thus see that it is uniformly continuous.This means that in δ-ε language :

here we manually set an interval in the domain. However, we are interested in the general relationship between two outputs without limitation ( other than the distance between two input must be in the range [0,1] ). So we want to now what happens when the |x -ξ| is larger than δ.
We recall the definition of norms in linear algebra. For finite vector space, the infinite norm is defined as:

It is easy to understand that this gives the largest entry (in terms of magnitude) of a vector. Note that this is true even if there exists more than one maximum entry. We expand this property into function space and define M to be the infinite norm of f(x). Then for |x -ξ| is larger than δ we write:

Then combine (3) and (4) we obtain

We now want to use this relation to show that Bernstein polynomials can be used to approximate f(x). We notice that the Bernstein polynomial of f(ξ) is just f(ξ), where binomial expansion has been used to obtain this result. Then, using the fact that Bernstein polynomial is linear for f(x),
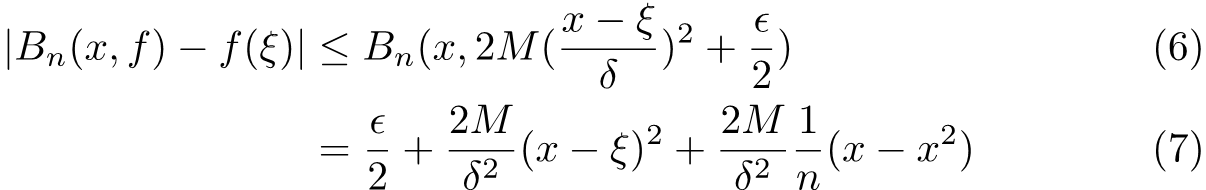 In the second line above we putted the first term of the function into the expression of the polynomial and it came out will some calculation. Obviously, we need to set x=ξ to proceed and this yields
In the second line above we putted the first term of the function into the expression of the polynomial and it came out will some calculation. Obviously, we need to set x=ξ to proceed and this yields

What does this means? Remember that we have the freedom to make n as large as we want. This means that we can make the difference between Bernstein polynomials and our function as arbitrarily small as we want by approaching n to infinity. i.e., Bernstein polynomials converges to our f(x).
[Literature: Matt Young, MATH 328 Notes, Queen’s University at Kingston, 2006]
2. Taylor’s Theorem
Now we are ready to prove Taylor’s Theorem. Knowing polynomials span the space of continuous function, we now assume that the function is also infinitely differentiable. In this special case, instead of using Bernstein polynomials, we want to use the basis consists of 1,x,…,xn. Matching the value of our series and our function at a particular point yields the ordinary form of single variable Taylor series.
3. Vector fields Taylor Expansion
To be continued…
Read Taylor’s Theorem in full

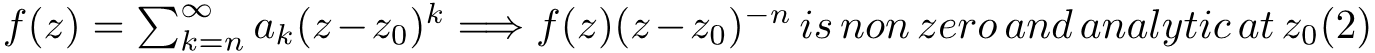
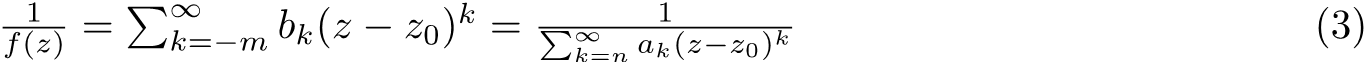
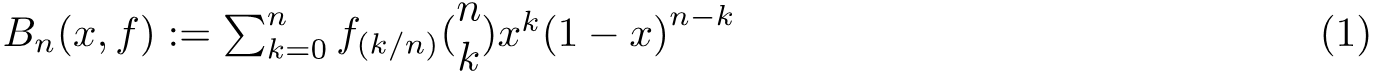



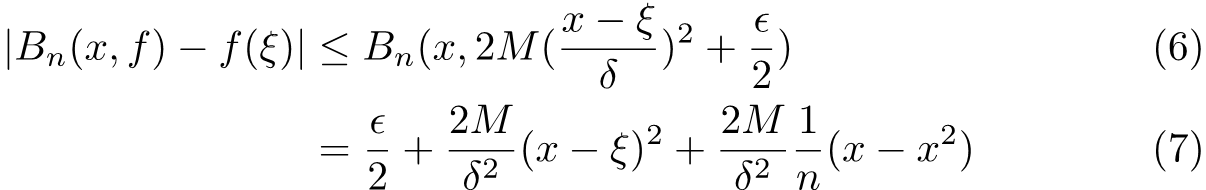 In the second line above we putted the first term of the function into the expression of the polynomial and it came out will some calculation. Obviously, we need to set x=ξ to proceed and this yields
In the second line above we putted the first term of the function into the expression of the polynomial and it came out will some calculation. Obviously, we need to set x=ξ to proceed and this yields