1. Start from the Abel-Jacobi-Liouville identity
Recall that if we have a set of differential equation:
![]()
The wronskian evolves as:
![]()
2. Liouville’s Theorem
Now we consider the a time independent Hamiltonian system (q,p). It satisfy:
![]()
Where F is a (n,2) matrix satisfying Hamilton equation for each pi and qi and n is the dimension of the space. This is an initial value problem and thus p and q depends on the initial set (q0,p0). Taking derivative for each component about the initial value and recombine, and use the fact that derivative w.r.t (q0,p0) commutes with time derivative gives:
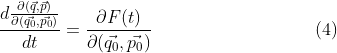
Evaluating the right hand side is a bit dizzy: For every component, for example, for the ith component of q, this is:
![]()
Now is the tricky part: Use the limit that when t is small:
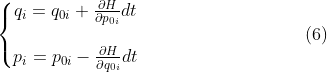
So the derivatives in (5) tends to zero apart from the derivative of the same component. We thus recognise from that (4) this is in fact, in similar structure to (1).
The trace of A is:
![]()
Thus the corresponding W, the Jacobian matrix of the mapping on the phase space between initial phase and the infinitesimal phase later, Has zero variation at the moment.
Importantly, one can easily show that W is 1 at the beginning. We can apply the same procedure starting from any successive moment and it will always give zero derivative: We thus conclude that W=1 all along and thus, the phase space volume conserved.
We observe that the condition that we can obtain this result is that the Hamiltonian is time independent. If not, an additional term will appears in (5) and it is not guaranteed to have trace of A cancelled in (7).




