Blog posts

Liouville’s Theorem of Phase Space

1. Start from the Abel-Jacobi-Liouville identity

Recall that if we have a set of differential equation:

The wronskian evolves as:

2. Liouville’s Theorem

Now we consider the a time independent Hamiltonian system (q,p). It satisfy:

Where F is a (n,2) matrix satisfying Hamilton equation for each pi and qi and n is the dimension of the space. This is an initial value problem and thus p and q depends on the initial set (q0,p0). Taking derivative for each component about the initial value  and recombine, and use the fact that derivative w.r.t (q0,p0) commutes with time derivative gives:

Evaluating the right hand side is a bit dizzy: For every component, for example, for the ith component of q, this is:

Now is the tricky part: Use the limit that when t is small:

So the derivatives in (5) tends to zero apart from the derivative of the same component. We thus recognise from that (4) this is in fact, in similar structure to (1).

The trace of A is:

 

Thus the corresponding W, the Jacobian matrix of the mapping on the phase space between initial phase and the infinitesimal phase later, Has zero variation at the moment.

Importantly, one can easily show that W is 1 at the beginning. We can apply the same procedure starting from any successive moment and it will always give zero derivative: We thus conclude that W=1 all along and thus, the phase space volume conserved.

We observe that the condition that we can obtain this result is that the Hamiltonian is time independent. If not,  an additional term  will appears in (5) and it is not guaranteed to have trace of A cancelled in (7).

 

 

 

Change of basis of a linear map

1. Coordinate maps

consider a random vector a. If the values of every entry are explicitly given, one could naturally identify it as a vector under the orthonormal basis. However, it could also been understood as the coordinate vector, which represents a vector under another basis by a coordinate map:

2. Change of basis of a linear map

Now we consider a linear map (represented by a matrix) A. It could be interpreted  as:

What if we want to change the basis of the objective vector space of f ? The following relation is obvious, if we want to find a matrix A’ representing the map after change of basis:

Where P is defined as a matrix that perform this basis change.

[Literature: Andre Lukas, Lecture note on Vectors and Matrices, University of Oxford]

3. The invariant map

Suppose we have a map that is invariant under any basis change, that is:

In other words, we would like to find an operator that commutes with any other operator on the same vector space V. Suppose now we have a vector x in V. We would like to find a non-trivial linear functional on x, so that we can define a linear map:

This is possible, for a functional in a n dimensional space can be express in to an (1 x n) matrix, so the left hand side can be expressed as (nx1)(1xn)(nx1) corresponding to v, f, and x respectively, and the former 2 combined and form a matrix. ( My reference mentioned ” Axiom of choice” with respect to finding non-trivial functional, and yet I have not understood it perfectly)

Then, the commutation relation implies:

Note that f(Tx), according to our pervious argument, should exist and independent on v. Thus, what we are doing consequently is that we have constructed linear maps P according to our need (that is, the vector v). In other words, we can assign every vector v in V a matrix P and they have to satisfy (6).

Then this inplies:

i.e. T is the scalar multiple of  the identity.

[Literature: Robert Isreal, https://math.stackexchange.com/questions/27808/a-linear-operator-commuting-with-all-such-operators-is-a-scalar-multiple-of-the]

 

Linear Functionals

1.Vectors

It is important to formalised the definition of a vector and a vector space. Here I shall pay no more attention on the this issue. But they are important as they characterised the condition that, for example, the scalar field accompanying with V, must satisfy.

1.Functionals

One should be very familiar with the definition of “linear” and “linear maps”(And from the definition we see linear maps can from a linear space: space of linear functions, as well). Very interestingly, we can show the following two important relations: for f: V→W:(See reference)

and that if ker= {0}, f: V→V is isomorphism.

We can get the following observation: consider a linear map with dim(imf) = 1 (Which, since vector spaces are defined base on a scalar field, this 1 dimensional space is the field itself. We name this special type of map linear functionals. Since we know that linear functions themselves form a vector space, we call it dual space V *(n,K) , this apply to linear functionals as well. Form (1) we know that one particular functional actually only act on one specific dimension, we conclude that there are only dim(V) types of linearly independent functionals. i.e. dim(V)=dim(V*). It follows that for basis {e} in V and basis {g} in V*, we naturally pair them together:

So that V and V* are putted in an equal status (symmetry).

Now, suppose we have f: V→W and g: W→F where g is a functional, it is easy to find the a functional in V*, namely, g( f ).  Then, we could also define another space of functionals h: W*→V* as h: g→f = h(g). 

We can also define a map i: V→V* and we can show the condition for it to be isomorphism. Since dimV = dim V* if we also know Ker(i) = 0 this should do it. Remember that for defining a dual space, it is necessary to recall that it represents a space of linear maps.  For any non-zero v, if w = f(v) is non zero (Note that the image of zero is always zero) the corresponding dual vector is (by our definition) non zero. (In other word, this map is not degenerate) However, we shall note that the proportionality between e and image of e by g is not restricted. We could try to more specify it:

Consider the effect on w, we also use it to define the inner product <,>: V x V→F:

[Reference: Geometry, Topology and Physics. M Nakahara(2003)]

Russell’s Paradox

1. The earliest from: Burali-Forti’s paradox

Though this form is only a subset of a general Russel’s paradox (from self reference), I have collected it for it involves an interesting concept in sets: The Ordinals.

We define a set to be an ordinal if it is hereditarily well-founded and hereditarily transitive. Hereditariness is defined as the specific characteristic of the set is inherited by every element of the set, and transitive is defined as the element of the element of a set is still the element of this set.

The direct observation of an ordinal O is that any element, sub element…etc. are all an element of O. Further more, any smallest indivisible element inside O is an element of O. Importantly, we immediately recognise that the set of all ordinals is, itself an ordinal (Let’s call it U ).

This property of ordinals make it possible to give well-defined orders in them. for example, consider an order type that rank each indivisible element, combined with the order type that rank the cardinality of sets (in terms of indivisible elements). In this way, U should be in a highest rank, higher than any element in U, includes itself.

2. Naive set theory and Russell’s paradox

The way that Russell spotted the paradox was through the unrestrictive comprehension axiom. This says that two formula f and g are identical iff f(x)= g(x) for any x. In this way we can construct a set {x: f(x)} to collect all x satisfying formula f(x).

Russell took f(x) as x is not an element of x. Then R= {x: f(x)} seems to be both an element and not an element of this set. This leads to a contradiction

3. Solutions to Russell’s paradox

Let us rewrite what Naive set theory gives us in a tidier mathematical form:

Russell’s response is call typed theory. This came from vicious circle principle stating that ” no proposition function can be defined in prior to specifying the function’s scope of application. Thus (1) should be modified:

Here S should be restrict x s.t. εf is not impredicative. R is defined in such a way that εf is impredictive so according to (2)  no such a set A exist.

Typed method, effectively, simple denies the set described by “all possible…., universal…” to be a set. However, there are other responses to the paradox. For instance, the axiom schema of Separation states that:

This is in similar manner to (3) but it does not directly state what set A should be. But now take f to be the one in Russell’s paradox gives the result of A does not exist.

Other arguments wanted to do it in different manner. Intuitionism and Para-consistency seems to be admit the existence of true contradiction and they altered some basic sentential logic. What are their relation to dialectics? I will come to that later.

[Reference: Stanford Encyclopedia of Philosophy: Russell’s Paradox]

 

Basic Thermodynamics

At the very, very beginning, let us see what thermodynamics up to: This is a science investigate the 1. To which forms energy goes to, and 2. how to make energy useful. Let us start from the first issue. It is a common-sense that energy consists of mainly to forms: (ability to do) Work and (ability to release) Heat. The former one corresponds to a directed, ordered moving, in contrast the latter shows a chaotic movements (in statistical physical sense). 

Thus we have the first law. It said that the change in total energy should be decomposed to heat and work. 

Since industrial revolution, the requirement of human on work rapidly increases, even (say) exceed the need on heat. This relates to the second objective of  thermodynamics: How to make energy useful. More specifically, we wanted to discover the convection laws better work and heat. 

To achieve that, we first need to identify what energies are useful. One may dream of convert thermal energy to work with infinitesimal cost, or in other word, convert an object’s thermal energy completely to work. However, this is not that useful  (and, in fact, impossible) : one need to “recycle” the row material , that is why we are interest in thermodynamical “cycles”. We wish for each cycle, the working substance can come back to its original “state” (For a state, we tried to find all what we called states variables that thermodynamically we cannot tell the difference between two substances with identical values of state variables). Our task is thus, identify the condition which a completely restored to the original state, while making useful effect, is possible. 

It is a common-sense that under some conditions our processes are dissipative, i.e. energy flow out regardless either direction we undergo in the process. Dissipative work includes friction, and dissipative heat includes heat lost. For instance, say we have a random process that involve (mechanical)work done. Let us further assume that the process involve at least one (either pressure of the object or the pressure of the surrounding) well-defined pressure. Whatever the process is, if originally (without friction) we expect the process can go back to the original state (both system and surrounding)  following the same path (We call this reversible), this time with friction we have the pressure deviated higher from the path in the forward process and deviated lower from the path  in the reverse process. This means it is no more reversible. Similarly, processes involving heat dissipation are again, irreversible. (We can show it quite generally)

There are other processes without dissipation that are irreversible. But as we have found out, reversible processes guaranteed non-dissipative nature, it means that we should be interested in these processes. Thanks to the study in heat engine by Carnot, we have a well-establish example of reversible processes: Carnot cycles. From the definition of Carnot cycle and another important statement: The second law of thermodynamics, one can derive the complete picture of basic thermodynamics, as we will discuss later.

One easiest approach to the second law is using microscopic point of view (Although is had not been understood by the physicists in the 19th century yet): Through a diffusion process, heat can indeed only spontaneously flow from hotter to colder objects, not reverse. This is Clausius’s statement of the second law. One can show that it is equivalent to the Kelvin-Plank’s statement. Using Clausius’s statement, one concludes that a reversible heat cycle operating between two reservoirs (apart from the trivial one: The one goes back to the starting point with identical path) should have the same efficiency as the Carnot’s cycle, which is naturally a maximum efficiency one can achieve as a heat engine. Reversible heat cycles as we defined, are thus indeed the most particular type of cycles (and in fact are fictitious) and are indeed the type we are seeking. 

Either using the efficiency relation (require the process is quasi static so that we can draw a path) or using the Kelvin’s statement, we can derive Clausius’s theorem for any closed cycle. On the other hand, it is easy to observe that any two points on the P-T-V diagram can be connected by reversible processes (If a states equation exist). Thus we can use Clausius Theorem to induce that for any two points on P-T-V diagram there exist a fixed quantity, if we set the quantity at one point is zero, then this quantity is well-defined in the entire space and independent on the path — from now on we call it entropy. 

Since entropy and  internal energy are both state variables, from the first law we conclude that for irreversible process, heat is always less than the corresponding reversible heat and thus work, must be greater than the corresponding reversible work. 

Zeros and Poles

We will briefly discuss zeros and poles of meromorphic functions here. We assume the Laurent series exist in the vicinity of a point z0:

Clearly if we want f(z0) is zero we require ak is zero for k smaller and equals to zero. Consequently we define that z0 is a zero of order n if:

We can observe some useful properties from (2). Firstly, an n order zero implies that up to the (n-1)th derivative of f(z) are also zero at z0 and vice versa. We can use this property to determine the order of zeros of a function, in the case that they are not so obvious. Secondly, The zeros of f(z) are the poles of 1/f(z) for obvious reason, provided that f(z) is not identically zero. We would like to find the properties of the Laurent series of  1/f(z):

The value of m can be determined by multiply the denominator of right hand side : We obtain a series that constantly equals to one. This requires m=n, and we see the coefficients bk are fixed by the values of ak .

In summary we found that

In particular, if f(z) is analytic and non-zero at z0 , we now from (2) know that n=0 and thus from (4) 1/f(z) is also analytic and non-zero at z0.

Introduction&Instructions

Hi, this is Cocteau. I hope this message finds you well.

Here, Cocteaupedia is a website where I store my thoughts and notes on Mathematics and Theoretical Physics. I like to imagine that the mind of an individual human is a little universe. Formulating my learning traces is my way of constructing this universe, and part of my ultimate goal is to understand the grand universe through the reflections of my little universe. What a cute thing!

Before Cocteaupedia was created, I was mostly building this universe on papers. However, due to my perfectionism I found that for me, it can be very hard to keep the note been taking, without starting to rubbishing them. As a result I frequently end my old plan and restart a new plan, and gradually I felt that this was neither meaningful nor eco-friendly (in terms of the amount of paper I have wasted).

Creating digital notes largely solves this issue, and a website is the optimal choice: it can be accessed at any spacetime, and is readily available to be shared and discussed. This is the story of why I created Cocteaupedia.

On this platform, every post is related to a specific question I’ve asked while learning maths and physics. For instance, the ideal of a post can be initiated when I was wondering the origin of Schrödinger’s  equation, or when I tried to think about how to calculate the residue of 1/ez+1 . I will try to organize them into topics and subtopics, displayed as Categories. For each post, important concepts that aren’t explained will be highlighted in bold. Only lengthy formulas will be written in LaTeX and displaced as pictures. This is due to display issues, which force me to write short, in-text mathematical relations or definitions – which are less necessary to be displayed as formulas – in regular text. Italic and bolded text will be used for emphasis.

There are, for now, no further instructions necessary to ensure smooth reading of the posts.

Thank you for reading this, I hope Cocteaupedia can be a good piece of work for you.

Cocteau

Created 20 May 2023

Modified 29 May 2023

[Homepage picture: Wikipedia-String Theory]

Taylor’s Theorem

1. Weierstrass Approximation Theorem

We want to show that The set of polynomials is dense in the space of continuous functions. We shall firstly define the Bernstein Polynomials as

where f is a continuous function with domain [0,1] and we can thus see that it is uniformly continuous.This means that in δ-ε language :

here we manually set an interval in the domain. However, we are interested in the general relationship between two outputs without limitation ( other than the distance between two input must be in the range [0,1] ). So we want to now what happens when the |x -ξ| is larger than δ.

We recall the definition of norms in linear algebra. For finite vector space, the infinite norm is defined as:

It is easy to understand that this gives the largest entry (in terms of magnitude) of a vector. Note that this is true even if there exists more than one maximum entry. We expand this property into function space and define M to be the infinite norm of f(x). Then for |x -ξ| is larger than δ we write:

Then combine (3) and (4) we obtain

We now want to use this relation to show that Bernstein polynomials can be used to approximate f(x). We notice that the Bernstein polynomial of f(ξ) is just f(ξ), where binomial expansion has been used to obtain this result. Then, using the fact that Bernstein polynomial is linear for f(x),

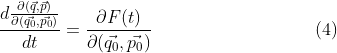
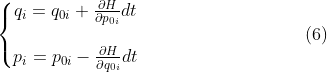
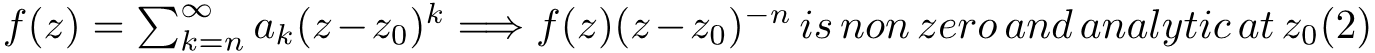
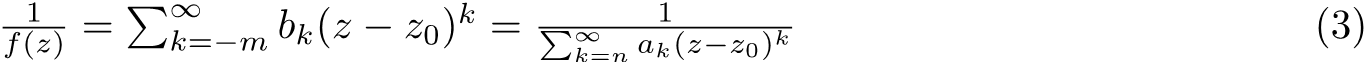
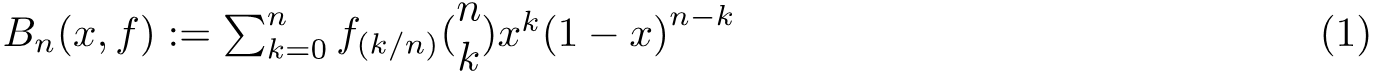
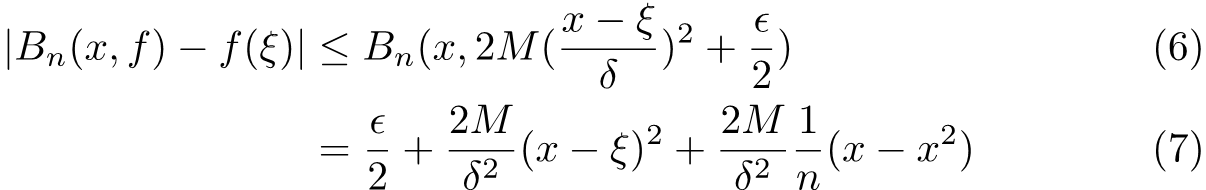In the second line above we putted the first term of the function into the expression of the polynomial and it came out will some calculation. Obviously, we need to set x=ξ to proceed and this yields

What does this means? Remember that we have the freedom to make n as large as we want. This means that we can make the difference between Bernstein polynomials and our function as arbitrarily small as we want by approaching n to infinity.  i.e., Bernstein  polynomials converges to our f(x).

[Literature: Matt Young, MATH 328 Notes, Queen’s University at Kingston, 2006]

2. Taylor’s Theorem

Now we are ready to prove Taylor’s Theorem. Knowing polynomials span the space of continuous function, we now assume that the function is also infinitely differentiable. In this special case, instead of using Bernstein polynomials, we want to use the basis consists of 1,x,…,xn. Matching the value of our series and our function at a particular point yields the ordinary form of single variable Taylor series.

3. Vector fields Taylor Expansion

To be continued…

 

Wronskian

1. Derivative of a determinant

Consider the determinant W(t) of a n×n matrix Y which each element is a function of t. Assume elements to be independent variables. Then we could write:

Where Cij are the corresponding cofactors. Thus we have:

Let’s define γi as the new matrices form by substituting the ith row with its derivative. Then we could write (2) in a tidier form:

2. Abel-Jacobi-Liouville identity

As we know, any system of linear ordinary equations can be extracted in to a single linear equation, namely:

And it is followed by that,

So we obseverve that a particular row of the derivative is the linear combination of the original rows, since for the kth row of Y, different elements on jth column are multiplied by the same factor Aik. So of course, each term on the right hand side of (3) will be W times the corresponding element of Aii.
Thus,

This has resulted in some interesting conclusions. For example if the solutions are independent for any point within the domin, they must be independent entirely.

[Literature: Pontryagain 1962, Chapter 3]