Thomas Walker is a second-year student at Imperial College studying for a BSc in Mathematics with Statistics.
Earlier this year, Prime Minister Rishi Sunak announced his plans to make the studying of mathematics compulsory until the age of 18, making it a central part of the UK’s future education strategy. He emphasised that focusing on numerical literacy is essential for future economic and societal development. But will his plans work?

Sunak’s strategy is, in part, motivated by the fact that the UK lags many of its European and Asian counterparts when it comes to average numeracy. Some surveys even show that up to half of the working-age population in England has the numeracy level that we would expect from primary school children.
What is mathematics, really?
Some may say that mathematics is just a collection of theorems and definitions used to describe physical phenomena. However, my perspective is that these are just the products of mathematics. For me, mathematics is a framework for thinking. It is a method of formalising ideas so that they can manifest in the real world. A mathematician is not an encyclopaedia of theorems, they are a rigorous explorer of their imagination.
Someone who says that they are not good at mathematics because they cannot remember their multiplication tables, I believe, has misunderstood the true nature of mathematics. A mathematical thinker does not need to remember the syllable of every theorem or the digits of pi.
A mathematical thinker should be able to reason from first principles. They can follow logical channels to reach theoretically grounded conclusions. Mathematics is about learning how to navigate this abstract terrain and utilise it for real-world applications.
In my experience with tutoring mathematics to secondary school students, it is apparent that this perspective of mathematics is not emphasised enough. Instead, teachers insist that their students memorise mathematical results, like equations, with a general lack of appreciation for the underlying principles.
My favourite concept to explain to a student studying A-level mathematics is the geometrical interpretation of the determinant of a matrix. A matrix is a mathematical object that stores numbers in rows and columns. A table in Excel is a type of matrix, for instance, though a table can only store information in rows or columns while matrices can input values for both.
Often, students are asked to calculate the ‘determinant’ of a square matrix (a matrix with the same number of columns and rows… 2×2, 3×3 etc.) Students often just memorise this simple calculation but never question what the determinant actually is. It is actually packed with geometrical information that is a bit too involved to explain in this blog post, but most students will only ever blindly calculate it to score marks on an exam.
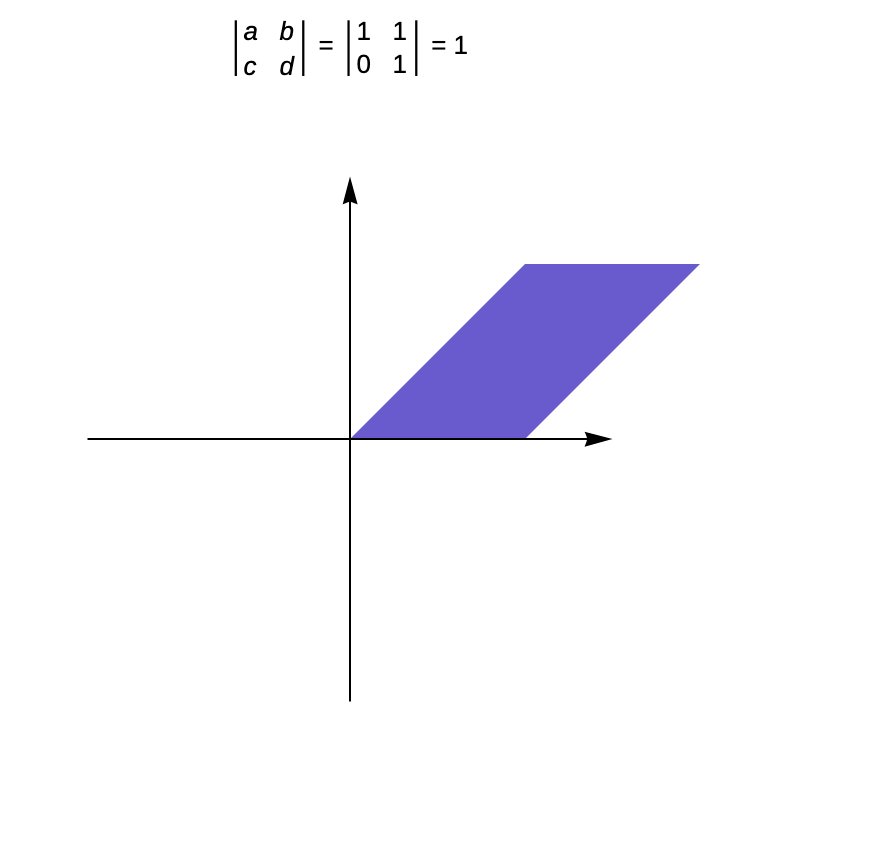
For me, learning these insights developed my appreciation for the subject and ignited a passion to teach mathematics to others.
The current style of teaching in schools is a regression from the way mathematics was taught in the past by thinkers such as Archimedes, where mathematics was just an extension of abstract thinking and formulation. I think this is one of the underlying reasons why a negative stigma around mathematics has developed.
Students find it frustrating when they are not able to remember concepts, and as a result, they get increasingly annoyed at the subject. It is clear to me that mandating the study of mathematics in its current form will not fix this issue.
What would get students to improve at mathematics?
It is not natural to unload mathematical concepts onto students. Mathematics was developed from thinking critically about the world and it should be in this vein that it is taught to students.
Suppose you are confronted with the task of calculating 18 per cent of 50. Some may try and do this with a calculator, or work through the calculations with a pen and paper. However, someone with an astute knowledge of proportions may realise that this problem is equivalent to calculating 50 per cent of 18, which is considerably easier.
This sort of intuition is gained from understanding proportions from a conceptual perspective rather than a perspective based on calculations, it is the former perspective I believe should be emphasised in the design of mathematical curriculums.
Rishi Sunak’s reforms makes it compulsory to study mathematics to the age of 18, and there are planned efforts to also increase the resources available to students and teachers.
As a mathematics student, I am in favour of promoting the learning of mathematics, and some of these measures are encouraging. For example, enhancing the pool of available programs for 16-18-year-olds can help expose students to mathematics that is useful in their day-to-day life. This will help alleviate the current concern of many students that the mathematics being taught has no real-world applications.
However, it is also apparent that there is a lack of resources available to younger children. Parents are seeking greater focus on solutions targeting the education of young school children, rather than trying to rectify the problems by prolonging the study of mathematics.

I can understand the concerns of the parents and realise the need to reform the learning experience of younger students. If the culture is not fixed for early levels of education, then the proposals that target the later stages of education will be less effective, and potentially even counterproductive.
I strongly believe in fostering an environment in which students appreciate learning mathematics for its elegance rather than to pass exams. Mathematics in its purest form is an incredibly creative subject. Younger students have a remarkable capacity for creativity which the mathematical curriculum should aim to express.
A great example of a way to promote mathematical creativity is the United Kingdom Mathematics Trust’s mathematical challenges, which stretches students to solve questions that do not follow the same patterns of normal exam questions. It challenges students to think about what they learn in new and interesting contexts.
Transitioning to university
The transition I experienced from A-level mathematics to undergraduate mathematics was stark. Mathematics at university requires different methods of thinking. At university, there is a greater emphasis on thinking from first principles and understanding ideas at a fundamental level so that you can extrapolate concepts into different domains.
You are required to think methodically to ensure that you construct rigorous arguments. You are encouraged to be curious and test the boundaries of your knowledge. At university you are not just taught mathematical theories, you are taught methods; ways of thinking are emphasised to equip you with the capacity to explore the vastness of mathematics.
Mathematical ideas have been developed over millennia; no number of courses will expose you to its entirety.
Mathematics has given me the confidence to explore computational learning theory and the mathematics of machine learning. Topics whose roots lie in the rigour of mathematics but grow and branch into the field of computer science. Mathematics should equip individuals with the confidence to trek their own path.