PhD student José Giral Barajas explains how he is using queueing theory to understand how cells move and accumulate materials.

Imagine you need to deliver a package to someone in a crowded place, but you have no idea where they are. No matter how determined you are to take a specific path, the constant collisions with all the people around you will force you to change direction most of the time. The path you take in your search for the recipient becomes effectively random. This simple picture is a helpful way to think about how cells move materials.
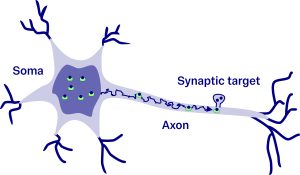
Inside a neurone, macromolecules and organelles are enclosed by a membrane forming a small compartment called vesicle and transported from the soma along the axon to synaptic terminals. Each delivery takes a random time because the environment within the cell is noisy. Once a vesicle arrives, it is eventually utilised by the neurone. This continuous interplay between delivery and consumption determines whether resources at the synaptic terminal blow up to infinity or settle around an equilibrium.
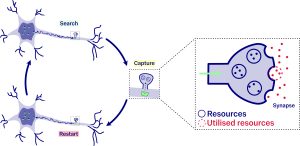
Our mathematical lenses: queues and first-passage times
I am a PhD student in Applied Mathematics at Imperial, supervised by Professor Paul C. Bressloff. In our research project, we model the accumulation of cellular resources as a combination of intracellular transport and consumption, viewed as a process that evolves randomly over time. These types of processes, with random evolution, are known as stochastic processes. Our aim is to contribute to the development of a mathematical framework that explains how precise transport, delivery, and consumption of cellular resources emerge from random and chaotic cellular interactions. We explore this by combining ideas from two types of stochastic processes: first-passage processes and queueing processes.
Queuing processes enable us to study how randomly arriving customers accumulate within a system that provides them with some service on a random basis. Imagine a supermarket where customers arrive at the checkout queue randomly, as they finish selecting their products. Additionally, once they reach the checkout area, they take a random amount of time to scan and pay for all their items. This thought experiment serves as an example of a queueing process and can be generalised to many phenomena.
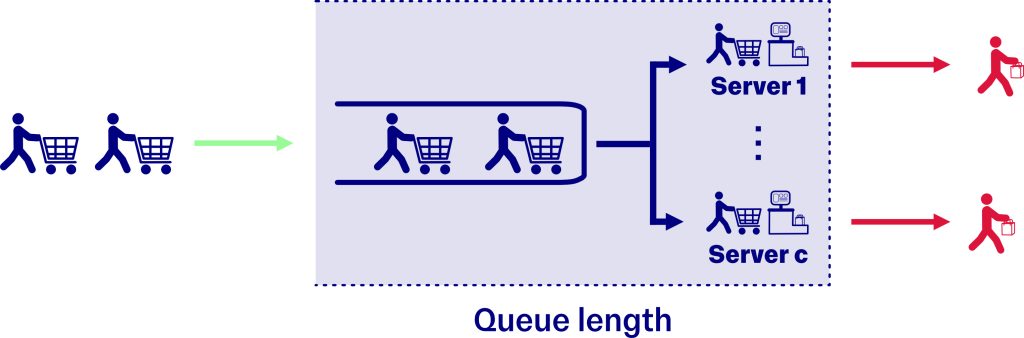
First-passage processes allow us to study the time it takes a customer to find the checkout tills when they are randomly searching for them. Now, imagine that each customer wanders through the supermarket, looking for the tills, choosing randomly which aisle to turn down. The time each customer takes to find the tills is random and depends on the size of the supermarket and where they started their search. Combining first-passage processes with queueing processes enables us to study the long-term accumulation of resources within the queue, depending on the shape of the supermarket and the initial position of the searchers.
Mapping biology onto mathematics
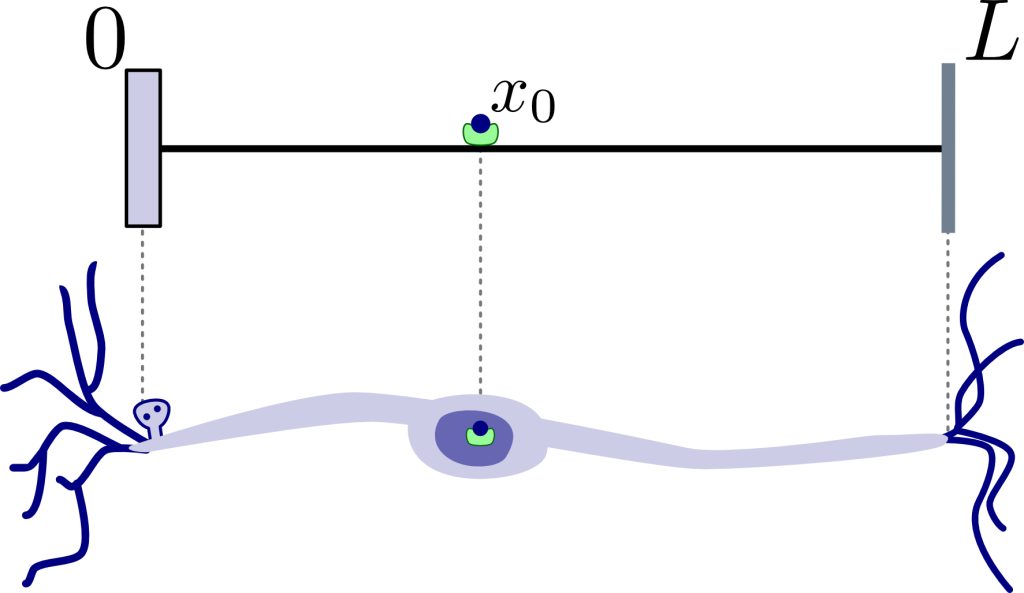
Due to the thin, elongated shape of the axon, we make the—not entirely realistic, but mathematically sound—assumption that the search takes place along a straight line of length L. This length, L, represents some physical constraint on how far the search can reach, for example, the length of the axon. The synaptic target sits at the start of this line, and the end represents an impenetrable boundary that reflects the searcher into the line. Thus, each time the searcher reaches the end of the line, it is reflected in the opposite direction, and each time the searcher reaches the start of the line, it delivers resources to the synaptic target. Each resource begins its journey at the soma, sitting at a fixed position, x0, inside the line.
Microscopically, vesicles are transported by molecular motors that depart from the soma. However, the molecular motor is bombarded with impacts from the particles crowding its environment. The bombardment of impacts on the molecular motor causes its motion to become erratic and random. This erratic and random motion, generated through multiple random collisions of molecules, is known as Brownian motion. In our model, resources are transported via Brownian motion as they search for their synaptic target. Each time the target is reached, it captures the resources, and the molecular motor returns to the soma to reload a new vesicle and restart the process. The repetition of these three steps generates a sequence of times marking the delivery of resources to the synaptic target.
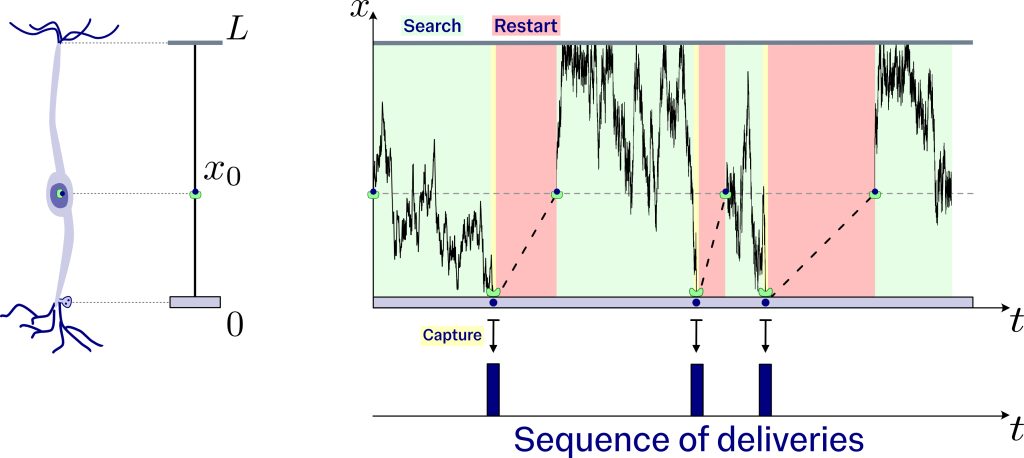
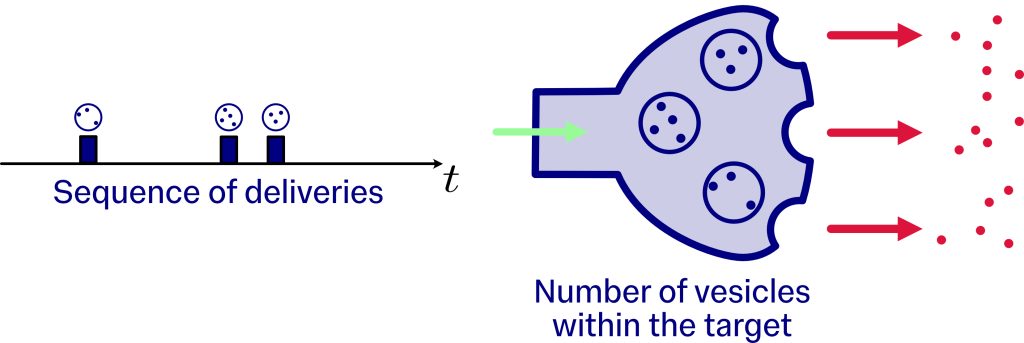
This sequence of deliveries determines how customers arrive at the queue, similar to how shoppers enter a checkout line in a supermarket. In this case, we associate the queue with the synaptic target and the customers with the vesicles, which arrive according to the times obtained in the search process described earlier. The vesicles accumulate within the synaptic target as they arrive. However, when a vesicle finds an active site on the membrane, after waiting a random time, it releases its cargo into the synapse.
Pathological blowup vs healthy equilibrium
Having defined the model, we exploit the results from queueing theory and first-passage processes to understand how the number of vesicles within the synaptic target will behave. Queuing theory provides a simple criterion for determining whether the long-term number of vesicles at the synaptic target will remain balanced or whether it will grow uncontrollably to infinity. If the arrival rate of vesicles is smaller than the total consumption rate, the long-term number of vesicles at the synaptic target settles to a stationary distribution. Otherwise, if the arrival rate is equal to or greater than the departure rate, the number of vesicles within the synaptic target will grow without bound as time progresses. The later scenario, in which the resources in the queue grow without limit, is usually called blow up.
On the other hand, first-passage theory allows us to compute the long-term arrival rate of vesicles at the synaptic target in terms of the geometrical features of the system—the axon’s length and the soma’s position. Combining the two results, we obtain a critical distance between the soma and the synaptic target that separates the long-term behaviour of the number of vesicles within the synaptic target into two regimes. When the soma is farther than this critical distance, the synaptic target can clear incoming vesicles and reach an equilibrium. When the soma is closer, deliveries occur too quickly, and the number of vesicles within the synaptic target increases rapidly, approaching infinity.
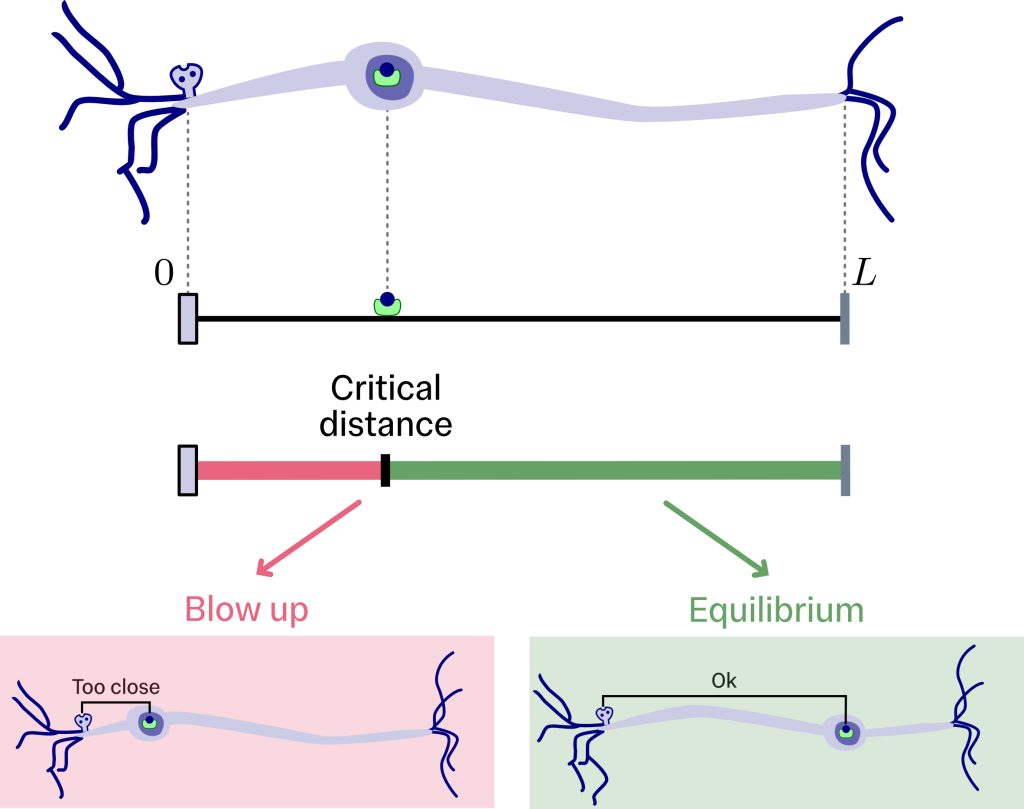
This first, simple result provides a rich insight: when the transport is assumed to be random, the spatial configuration of the neurone can alone determine whether resource levels at the synaptic target remain balanced and healthy or blow up into excess. This excessive accumulation of resources within the synaptic target may trigger neurodegenerative diseases. But many realistic features remain to be incorporated into this model and explored.
There are several natural extensions of the model we would like to explore. We aim to move beyond one dimension and investigate how arrival times and accumulation change in two-dimensional and three-dimensional geometries. There is also space for more realistic stochastic motions than the Brownian motion. What if transport is not purely random but combines active runs with random directional switching? Typically, there are multiple motors delivering resources to multiple synaptic targets. Therefore, we plan to explore how geometry affects resource accumulation in multiple synaptic targets that receive resources from multiple interacting searching motors. Each extension presents new mathematical challenges and may provide new biological insights, so there is still much to be explored!